図１０で、各原子の質量をm、原子間のバネ定数をS、原子の配列間隔をＬ、第n番目の原子の平衡位置からの変位量をunとすると、運動方程式は、

【式２】

となります。

図１は、図１０の単純化されたモデルと等価であると上では述べましたが、パッシブラジエータの質量m0に加えて空洞３内の空気の質量を考慮し、さらに空洞３内の空気の弾性に加えてパッシブラジエータ自身が持つ（エッジやダンパ等の）バネ定数S0を考慮すると分散関係は、

【式１０】

と書けます。

式（２）は、

【式３】

の形のいわゆる進行波型の解を持っています。ここで、kは波数、xは質点とバネの配列方向に沿う位置座標、ωは角振動数を表します。

式（３）で表される波動が、空気中を伝搬する通常の音波とは全く異なる挙動を示すことは、以下の数式、

【 式 ４】

【 式 ５】

および式（３）を上の式（２）に代入して得られる分散関係（*1）、

【 式 ６】

を通じて理解することが出来ます。

（*1：物理系の分野では周波数によって伝搬速度が違うことを「分散」と言いますが、同じことを電気系の分野では「群遅延」と呼ぶようですね。）

式（６）においてωは、波数kに対して単調に増加し、

【 式 ７】

で最大値をとります。

また、空気中の音速がほぼ一定であるのに対し、格子振動の位相速度Vpは、

【式８】

のように、質量mとバネ定数Sの値に依存して変化します。 その結果、質量mとバネ定数Sの値を適切に設定することにより、位相速度Vpを例えば空気中の音速よりも低く設定することも可能です。

さらに、式（８）は、位相速度Vpの周波数依存性を表していて、位相速度Vpの最大値が、

【式９】

であり、これよりも小さな波数（長い波長）において単調に減少することを示しています。

以上のように、音響ラティスを伝搬する波動は、

・2Lよりも短い波長の波動が実質的に伝搬しない

・位相速度Vpが質量mとバネ定数Sの値に依存して変化する

・位相速度Vpが周波数依存性を持っている

という点において、空気中を伝搬する通常の音波とは全く異なる挙動を示すものです。

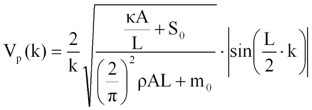
また、この場合の位相速度Vpは、

【式１１】

となります。

ここで、

A：管４の内断面積

κ：空気の体積弾性率

ρ：空気の密度

をそれぞれ表します。

例えば管４が内径0.08mの円筒管である場合を例として、各パラメータ値を以下のように設定すると、

A：0.005m2

L：0.2m

m0：0.014kg

S0：836N/m

κ：141700N/m2

ρ：1.29kg/m3

このとき、伝搬可能な最短波長２L（波数π／L）における格子振動の周波数は175Hzとなり、位相速度Vpは、70m/sと空気中の音速に対して約１／５の低速になります。また、波長４L（波数π／２L）における素子振動の周波数は62Hzとなり、位相速度Vpは、50m/sとなります。 音速が例えば約１／５になるということは、波長も約１／５になるということです。つまり同じ１周期の振幅が約１／５の距離に詰め込まれてしまうわけですから、このことは、音響ラティスを用いて共鳴管を構成すれば、その全長を大幅（上記の例では１／５以下）に短縮可能であることを意味します。

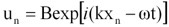
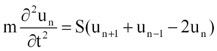
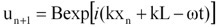
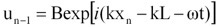
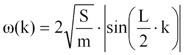
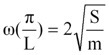
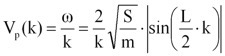
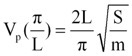
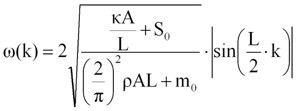
「ラティス（Lattice）」は「格子」を意味します。

そもそも音響ラティス技術の着想は、固体中の原子の振動現象にヒントを得ています。固体物理では、固体中の整然と配列した原子の並びを「格子」に例え、その並びを伝わる波動を「格子振動（Lattice vibration）」と呼びます。我々の身の回りの物体が温度を持っていることは、それらを構成する分子や原子が微視的に熱運動をしていることの現れであると説明されますが、「格子振動」は固体における熱運動の典型的な形態なのです。

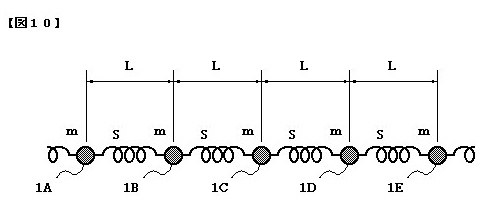
さて、固体中では原子同士が原子間力で結ばれて固体としての成り立ちを保っています。この様子を模式的に示したのが図１０です。図の１Ａ〜１Ｅは原子を表していて、その間を結ぶバネが原子間力を表しています。実際の固体は、このような配列が四方八方に張り巡らされたジャングルジムのような立体構造の格子を持っていますが、ここでは単純のため、その1辺だけを取りだしています（すなわち一次元的な格子です）。

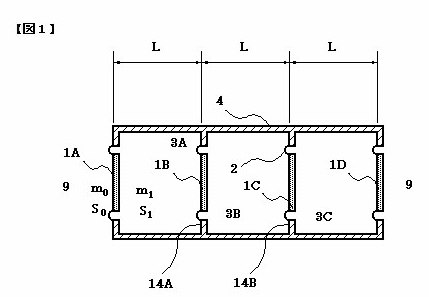
一方、下の図１は、Strataが採用する音響ラティスの断面構造を表した模式図です。筒状のキャビネット４の内部が、パッシブラジエータ１Ａ、１Ｂ、１Ｃ、１Ｄで区切られていて、その間が空洞３Ａ、３Ｂ、３Ｃになっています。パッシブラジエータの質量→原子の質量、空洞内の空気の弾性→バネの弾性、と見なせば、図１と図１０とは全く等価です。

図１０で、ある原子が振動すると、その動きがバネを通じて隣の原子を揺り動かします。そしてそれが更に隣の原子を揺り動かし・・・という具合に伝わって行くのが格子振動です。図１の場合には、あるパッシブラジエータの振動が隣接する空洞内の空気を圧縮伸長する結果、隣のパッシブラジエータを揺り動かします。そしてそれが更に隣のパッシブラジエータを揺り動かし・・・という具合です。

このようにして格子を伝わる振動の伝搬速度と波長には実は制限があります。空気中の音波であれば、高音から低音まで同じ音速で伝わって行きますが、格子振動や音響ラティスを伝わる振動の場合には、そうではないということです。

式（７）は、図１０においては原子とその両側Ｌ／２の領域内のバネで構成される長さLの領域が最小の振動単位であるために、隣り合う原子が逆方向に運動する波長2L（波数π／Ｌ）の振動が最短波長（すなわち最大波数）の伝搬モードであり、これよりも短い波長の格子振動が伝搬できないことに対応しています。

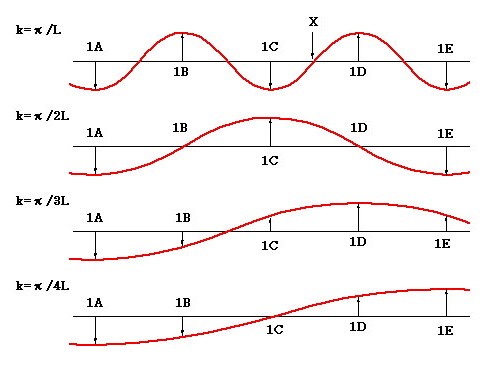
下に示したグラフは、波数がπ／Ｌ、π／２Ｌ、π／３Ｌおよびπ／４Ｌである各格子振動の変位を，図１０の１Ａ，１Ｂ，１Ｃ，１Ｄおよび１Ｅの各原子との位置対応においてプロットしたものであり、このグラフからも格子振動の波長が2Lよりも短い値となりえないことが理解できます。

ところで式（１１）は、L→0（同時にm0、S0も→0）の極限をとると空気中の音速に一致します。つまり音響ラティスの連続極限は、通常の共鳴管です。逆に、通常の共鳴管を離散化したものが音響ラティスであると考えることも出来ます。その離散化要素である振動板とバネの１組だけを切り出すと、それは通常のバスレフに代表される単一のHelmholtz共鳴系です。２組切り出せばダブルバスレフ、３組ならばトリプルバスレフ、そしてこの操作を無限に細かく繰り返して得られるのが通常の共鳴管というわけです。

このように音響ラティスという概念を導入すると、バスレフ方式と共鳴管とは１本の軸上に並べて考えることの出来る仲間であることが理解できます。つまり音響ラティスという概念は、これら旧来のエンクロージャー方式を特殊ケースとして包含する、より広い概念なのです。

おそらく、「バスレフ特有の音」だとか「共鳴管特有の音」といった方式固有の音に対するイメージをお持ちの方は少なくないと思いますが、実は音響ラティスという視点からは両者に区別や境界はありません。両者の間には広大な設計領域が手つかずのまま広がっていて、本来そこにあるのはバスレフでも共鳴管でもない音の世界です。

Strataは、この未開拓の設計領域に埋蔵されている、我々が今まで体験したことのない音を掘り起こし、皆様に提案してゆきたいと考えています。また同時に、この未開拓ゾーンが自作マニアの活躍の場となることを願い、そのためのツールを提供してゆきたいと考えています。